11268. Построение
остовных деревьев
Рассмотрим неориентированный
полный простой граф G из n вершин. Вершины графа G пронумерованы от 1 до
n. В частности, каждая пара различных вершин соединена одним
неориентированным ребром, поэтому граф содержит в точности n * (n
– 1) / 2 ребер.
Вам задано множество E, состоящее
из n – 3 ребер этого графа G. Точнее, вам даны два массива x и
y с n – 3 элемента каждый. Для каждого допустимого i (xi,
yi) является одним из ребер в E.
Остовное дерево графа G – это подмножество
из n – 1 ребра графа G, таких, что эти ребра соединяют все n
вершин. Ребра остовного дерева действительно образуют дерево, которое является
подграфом графа G и охватывает все его вершины.
Нас интересуют остовные деревья,
которые содержат все ребра заданного множества E. Найдите количество таких
остовных деревьев по модулю 987654323. Два остовных дерева различны, если
существует ребро G, принадлежащее одному из них, но не принадлежащее другому.
Вход. Первая строка содержит число n
(4 ≤ n ≤ 1000). Вторая и третья строки содержат массивы x
и y (1 ≤ xi, yi ≤ n)
длины n – 3 каждый.
Выход. Выведите количество остовных
деревьев по модулю 987654323.
|
Пример
входа 1 |
Пример
выхода 1 |
|
4 1 2 |
8 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
5 1 2 2 3 |
15 |
|
|
|
|
Пример
входа 3 |
Пример
выхода 3 |
|
6 1 1 2 2 3 3 |
0 |
РЕШЕНИЕ
графы – остовное дерево
Анализ алгоритма
Если подграф из n – 3 ребер содержит
цикл, то ответ 0.
Используя
систему непересекающихся множеств, выделим компоненты связности графа. Если входной
подграф не содержит циклов, то получим 3 компоненты связности. Пусть A, B, C – компоненты
связности, a,
b, c – их размеры. Нам
следует добавить в имеющийся подграф еще два ребра. Ребра должны соединять
вершины из разных компонент связности.

Если мы соединим
ребрами компоненты A и B, а также A и C, то количество
способов выбрать их равно a * b * a * c. Соответственно
если два ребра проводятся между компонентами A и B, и B и C, то выбрать их
можно a * b * b * c способами. Два
ребра можно также провести между компонентами A и C, и B и C. Число способов
выбрать два ребра таким образом равно a * b * c * c. Следовательно ответ равен
a * a * b * c + a * b * b * c + a * b * c * c = a * b * c * (a + b + c)
Пример
Рассмотрим первый
тест. Построим все возможные остовные деревья с ребром (1, 2). Их количество
равно 8.
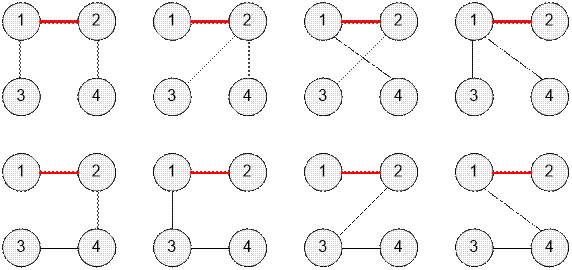
Заданный граф
содержит три компоненты связности с размерами 2, 1, 1. Количество остовных
деревьев равно
2 * 1 * 1 * (2 +
1 + 1) = 8
Во втором
примере три компоненты связности имеют размеры 3, 1, 1. Количество остовных
деревьев равно
3 * 1 * 1 * (3 +
1 + 1) = 15
В третьем
примере граф содержит цикл, поэтому ответ равен 0.
Реализация алгоритма
Объявим
константу – модуль MOD.
#define MOD 987654323
Объявим массив mas, используемый системой непересекающихся
множеств.
int mas[1001];
Функция Repr находит
представителя множества, в котором находится вершина n.
int Repr(int n)
{
if (n ==
mas[n]) return n;
return mas[n] =
Repr(mas[n]);
}
Функция Union объединяет множества, содержащие
элементы x и y.
int Union(int x, int y)
{
int x1 = Repr(x), y1 =
Repr(y);
mas[x1] = y1;
return (x1 != y1);
}
Основная часть программы. Читаем входные данные.
scanf("%d", &n);
vector<int> x(n);
for (i = 0; i < n - 3; i++)
scanf("%d", &x[i]);
vector<int> y(n);
for (i = 0; i < n - 3; i++)
scanf("%d", &y[i]);
Инициализация массива mas.
for (int i = 1; i <= n; i++) mas[i] = i;
Для каждого ребра (xi, yi) запускаем
функцию Union
(xi, yi).
Строим
компоненты связности.
for (int i = 0; i < n - 3; i++)
Если вершины xi и yi уже принадлежат одной компоненте
связности, то после их объединения появится цикл. В таком случае выводим 0.
if (Union(x[i], y[i]) == 0)
{
printf("0\n");
return 0;
}
Если a – представитель некоторого
множества, то в m[a] подсчитаем
количество элементов в этом же множестве. Если в подграфе циклов нет, то получим три компоненты связности, при этом m[a] содержит размер
компоненты, в которой находится вершина a.
map<int, int> m;
for (int i = 1; i <= n; i++)
m[Repr(i)]++;
Скопируем размеры компонент связности графа в вектор v.
vector<long long> v;
for (auto x : m) v.push_back(x.second);
Вычисляем и выводим ответ.
int res = (v[0] * v[1] * v[2] * (v[0] + v[1] + v[2])) % MOD;
printf("%d\n", res);